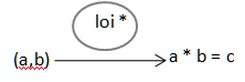concepts structurants #
des concepts opérants 3 : c'est pas pareil #Le contenu de la page
- c’est pas pareil
- quelque chose a changé
- dans des faits de tous les jours
- dans des objets du quotidien
- ça a changé comment ?
- des changements de propriétés
- des situations nouvelles
- les concepts sous-jacents
- l’erreur fructueuse
- quelque chose a changé
- changer : du constat à l’exploration et à la maîtrise
- représenter des relations
- faire fonctionner les fonctions
- appliquer les changements de propriétés
- transformer
- des changements particuliers : fonctions et lois numériques
- l’idée de détermination : si … alors
- définir la fonction
- quel changement ?
- comment le représenter ?
- définir la fonction avec précision
- faire fonctionner les lois
- composer, décomposer
- représenter la loi
- définir la loi
- changer le changement
- les fonctions et les lois
- de nouvelles fonctions
- de nouvelles transformations
- de nouvelles lois
- réitérer le changement
- annuler le changement : un retour au point de départ
- les fonctions et les lois
- de l’acte à la pensée
- créations formelles : et si …
- exploration des invariances
- c’est pareil ! des concepts
La perception des événements, objets ou situations, à travers le filtre « pareil/pas pareil » permet de mettre en évidence des caractéristiques communes ou distinctes et d’établir ainsi des relations entre les informations perçues, d’éveiller la curiosité, de susciter des remarques et des interrogations, ce qui conduit à l’émergence de problématiques spécifiques et à l’élaboration de démarches pour leur résolution.
La constatation, les tentatives de reproduction à l’identique ou de répétition du pareil engendrent des situations limites de « pareil, mais… », de « presque pareil ». Des objets, des situations diffèrent de peu, que par un détail, une propriété : ces deux stylos sont exactement les mêmes sauf pour la taille légèrement différente ; les ailes du papillon sont pareilles de chaque côté, mais « c’est à l’envers « .
L’étude des changements vécus, remarqués ou inventés ouvre la voie à la fréquentation de nouveaux domaines mathématiques et à leur exploration, que ce soit dans le champ non numérique ou numérique.
Ces recherches dans le monde non numérique, issues de faits de la vie quotidienne, n’ont pas pour seul but de créer des référents utiles, des « pré-requis » pour de futurs apprentissages numériques tels l’addition ou la multiplication. Elles constituent une activité mathématique à part entière, et ce, dès le plus jeune âge.
c’est pas pareil
quelque chose a changé
des faits de tous les jours
La fleur s’est fanée ;
On est passé dans un tunnel, il faisait tout noir ;
Le linge sale est passé dans la machine à laver. Maintenant il est propre.
D’où vient le vent aujourd’hui ? ;
Jean-Charles est allé chez le coiffeur ;
J’ai réchauffé ma soupe au micro-onde ;
Dans mon jardin, ça pousse ;
On a changé d’heure ;
L’année dernière, il y avait moins d’enfants dans la classe ;
Maman a eu un bébé : c’est une sœur ;
On a acheté une nouvelle voiture.
La fée a changé la citrouille en carrosse.
Quelque chose a changé, ça n’est plus pareil.
Qu’est-ce qui n’est pas pareil ? Qu’est-ce qui a changé ?
des objets du quotidien
|
deux stylos pas pareils |
les trousses presque pareilles |
|
La date au tableau : on observe des changements de couleurs et d’écritures. |
Les couleurs de la date, on dirait le drapeau de la France, mais deux couleurs ne sont pas à la même place.
|
|
Céline a eu une trousse de Disneyland et dedans il y avait une petite règle. Elle n’est pas pareille que la nôtre. |
Le livre Chipie : les chiens se tournent le dos. Les papillons se regardent. |
|
Le collier des perles du jour change chaque matin. |
les deux frères |
|
les décorations lumineuses de Noël dans les rues |
les pétales de la fleur |
|
Les deux amis Petit-Bleu et Petit-Jaune, quand ils se rencontrent, sont tellement contents de se voir qu’ils s’embrassent et deviennent… tout vert ! |
|
|
Amélie a apporté un coloriage qu’elle a fait à partir d’un modèle plus petit. |
» Ce matin, je me suis fait un chocolat. |
ça a changé comment ?
L’observation et la comparaison des objets révèlent des dissemblances pour certaines propriétés.
Cependant, les remarquer uniquement ne semble guère utile et maintient la situation au stade de simples constats. Se limiter à une énumération seule des propriétés peut figer la situation et mener à une impasse. Il est plus productif d’adopter une vision transformationnelle et de se focaliser sur l’étude des changements constatés.
La mathématique apparaît quand la description cesse.
Ces changements présentent une grande diversité. Ils peuvent être aléatoires et ne suivre aucune direction définie, ou alors être prévisible et fonctionnels.
des changements de propriétés
Parfois, ils sont simples et ne concernent que les critères d’une seule propriété : la taille (petit, moyen, grand, …), la couleur (rouge, bleu,…), la position, l’orientation.
Ce changement simple peut se répéter une ou plusieurs fois.
Il peut présenter une périodicité : les jours de la semaine ou les saisons.
Dans d’autres situations, plusieurs propriétés à la fois sont concernées . Leur combinaison plus complexe peut se répéter, s’alterner,…
Certaines variations sont soumises à condition(s) : « S’il pleut, alors l’escargot sort de sa coquille » ou « Si j’ai mes gants et mon bonnet, alors je peux faire l’activité patinoire ».
D’autres sont liées (covariances) : » A la pompe à essence, plus on remplit le réservoir et plus le prix augmente. » Ou inversement « Plus je mange de bonbons, moins il y en a dans le paquet ».
Des changements plus complexes, tel un arbre et son ombre, un objet et son reflet dans une cuillère, un dessin sur un ballon que l’on gonfle, opèrent dans certains événements. Ils sont étudiés dans le cadre de différentes géométries.
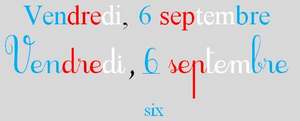 La date au tableau : on observe des changements de couleurs et d’écritures : script/ cursive, 6 en chiffre ou en lettres qui peuvent être réutilisés avec d’autres textes. |
Céline a eu une trousse de Disneyland et dedans il y avait une petite règle. Elle est plus petite que la nôtre. |
|
On a trouvé d’autres règles
…. comme ça |
Céline n’a pu s’empêcher de les ranger…
… puis comme ça |
|
Les trousses presque pareilles : un changement de couleurs qu’il faut décrire. |
Deux stylos pas pareils : il y a eu un changement de couleurs : |
|
Deux couleurs donnent naissance à une troisième. |
 Les couleurs de la date, on dirait le drapeau de la France. Il y a un changement de places à étudier. |
|
Il change de direction ou non. Il est intéressant d’essayer de reproduire fidèlement ces situations. |
 Les fleurs et les papillons ne sont pas disposés de la même façon. Tenter de reproduire ces phénomènes de miroir offre de prometteuses perspectives. |
|
Le nombre de flèches dans le carquois change mais une constante (3) apparaît. |
La flûte de Pan : chaque élément de l’instrument a une taille différente des autres. Il est tentant de créer d’autres flûtes de Pan… |
|
Le bracelet a des couleurs qui changent. Et si on inventait d’autres bracelets ? |
Le collier court (une grosse perle) remplace le collier long (dix petites) : ça change mais ça veut dire pareil. |
|
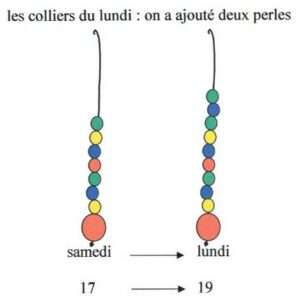
Lundi matin, le collier de la date ne change pas comme d’habitude. |
» Pour faire mon chocolat, j’ai pris du lait et j’ai ajouté du cacao. |
|
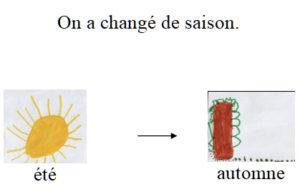
ça change mais ça se répète. Et si je change dix fois de saison ? |
Maxime varie la position des doigts sur les pistons de sa trompette. |
 Mathieu doit prendre 3 cachets. Il les avale un par un. Dans la main, il en a trois, puis deux, un et zéro. |
Les pétales de la fleur tournent. |
 Sur la montre, on voit une liste : 5, 10, 15, 20, 25 … Sur la montre, on voit une liste : 5, 10, 15, 20, 25 … |
et aussi deux listes de numéros qui changent : 1–>5 |
   d’autres associations de numéros |
des situations nouvelles
Certains changements sont le produit d’une composition d’éléments.
Le chocolat est le résultat d’un mélange de lait et de cacao.
L’arc-en-ciel nécessite la présence de pluie et de soleil.
La couleur verte est obtenue par le mélange de bleu et de jaune.
Le prénom Marie-Paule résulte de l’association de deux autres prénoms.
Ces situations non numériques sont du même ordre que des compositions comme 3 + 5 ou 12 : 4.
Ce sont les lois de composition qui permettent ces assemblages.
les concepts sous-jacents
| objet, situation | changements | concept sous-jacent* |
|
à la ducasse* la petite règle de Céline |
les stands : oui, non la taille |
relations relation d’ordre |
| les deux stylos les trousses |
changements de couleurs : bleu–>rose, gris –> gris |
fonctions non-numériques
périodiques
permutations |
| la date au tableau | script –> cursive, 6 –> six |
|
| le bracelet, les saisons | ça change en se répétant | |
| le drapeau | bleu-rouge-blanc –> bleu-blanc-rouge | |
| la trompette | position des doigt | combinatoire |
|
les flèches, les cachets
le collier des jours, du samedi au lundi la dent perdue |
Listes : 3,2,1,0 et 0,1,2,3
+1, +2 , +3 -1, x2 |
fonctions numériques croissantes, décroissantes,
additives multiplicatives
|
|
la coupe, le moustique, la décoration de Noël, le livre Chipie, le drôle de papa |
les « deux côtés » |
transformations géométriques
symétrie (axiale) |
| les poupées russes, la tour Eiffel, les T-shirts, les deux frères, Claire et sa soeur, la voiture miniature, la flûte de Pan | la taille | homothétie |
| le chien Chipie | la position | translation |
| les pétales de la fleur | ça a tourné | rotation |
| la grosse perle, les pièces | ça change mais ça veut dire pareil | égalité |
| Petit bleu et Petit jaune Le chocolat l’arc-en-ciel Marie-Paule |
(bleu et jaune) –> vert (lait, cacao) –> chocolat (soleil, pluie) –> arc-en-ciel (Marie, Paule) –> Marie-Paule |
loi de composition non numérique |
| 27 | (20,7) –> 27 |
loi de composition numérique addition |
* voir partie 2 « des recherches/la ducasse » et la partie 4 « domaines math/les propriétés, les relations »
** voir partie 4 « domaines math » les chapitres sur les fonctions. Nous avons appelé ce type de fonctions « avec constante » : y est associé à x quand une certaine propriété les lie, par exemple leur somme reste constante (x + y = 3 (les cachets, le dragon…), ou leur produit est constant etc. Donc en général quand leur composition à l’aide d’une loi * produit une constante : y = f(x) si x * y = constante.
Cette situation se produit également dans le monde non numérique : quand je mange une part de tarte, ce qu’il en reste dépend de la taille de ce qui est mangé. On est en présence d’une covariance avec constante.
l’erreur fructueuse
Des changements se manifestent parfois de manière imprévue : une consigne est donnée mais sa réalisation fait apparaître des erreurs. Des exemples :
– la couleur bleue doit être remplacée par du rouge mais la demande n’est pas toujours respectée : une erreur apparait et une fois, la couleur bleue est malencontreusement changée en vert ;
– le tracé d’un déplacement codé sur quadrillage : (3 ↑ et 2 → et 1↓ et 2 →) devient (3 ↑ et 2 → et 1↑ et 2 →)
– aujourd’hui, on est le 6 et Amélie a écrit 9 ;
– Pierre est interrogé et c’est Paul qui répond à sa place. Dans la classe, Paul est assis en face de Pierre.
– pour inventer sa liste de nombres, il en oublie deux à chaque fois : 1, 4, 7, 10, 13, 16, 18, 21, …
Toute situation dans laquelle une consigne donnée n’est pas respectée est susceptible d’offrir l’occasion d’étudier un nouveau changement. L’erreur d’exécution non prévue est prise en compte et érigée en nouvelle règle (on va se tromper comme…). Elle devient fructueuse, inductrice et créatrice.
– systématiquement, la couleur bleue devient verte ;
– tourner chaque chiffre, objet, … comme le 6 d’Amélie ;
– le nouveau jeu : Julie est interrogée, qui va répondre à sa place ?
– quelle liste obtient-on si on oublie trois nombres cette fois ?
De nouveaux changements apparaissent. Ce sont des changements de changements qu’il faut aussi examiner.
changer : du constat à l’exploration et à la maîtrise
La découverte d’un changement, à la suite d’un constat ou d’une erreur involontaire de reproduction, est une occasion de procéder à un nouveau questionnement, de réaliser une tentative de reproduction puis d’exploration. L’objectif est de maîtriser ce changement et de l’intégrer comme nouvelle connaissance.
représenter des relations
Un fait est relaté avec des mots : la fleur fanée, le passage dans un tunnel, la machine à laver, le micro onde, la nouvelle voiture, la fée…
Pour conserver l’événement ou pour le partager, il est nécessaire de produire une trace et d’opter pour un autre type de représentation : l’écriture du fait, un dessin, un schéma … D’autres possibilités que le graphisme existent : un témoignage sonore, visuel (photos, bande dessinée, mime, vidéo)… C’est le dessin qui est le plus souvent choisi.
Mais pour cela, il s’agit
– de préciser de quoi on parle, qu’est-ce qui change, d’isoler la/les variables en jeu :
un aspect plutôt qualitatif avec l’état de la fleur, la luminosité pour le tunnel, la propreté pour le linge, la chaleur pour le micro onde, l’objet en totalité pour la fée… ;
une nécessité plus quantitative pour « d’où vient le vent ? » (les directions cardinales, pour le coiffeur (accroissement de la taille des cheveux puis coupe), pour « ça pousse » (accroissement de la taille des plantes), pour le changement d’heure ou d’élèves dans la classe (numérique).
– de signifier le « avant/après », c’est à dire représenter du temps à l’aide de concepts spaciaux (droite/gauche, flèche…)
– d’expliquer comment ça a changé, de préciser les relations entre les variables (notion d’opérateur) *
* voir partie 4 « domaines math »
faire fonctionner les fonctions
Une fonction est une relation particulière qui associe un élément d’un ensemble de départ appelé antécédent ou objet, à un élément au plus d’un ensemble d’arrivée (appelé image), et toujours le même, ce qui élimine tout doute quant au résultat du changement.
Elle occupe ainsi une place privilégiée dans le monde des relations. Elle est très utilisée parce que efficace pour structurer des informations, relier et modéliser des ensembles de données, et faciliter la compréhension de phénomènes complexes.
Elle est associée à l’idée de détermination.*
* voir partie 4 « domaines math »
appliquer les changements de propriétés
Les couleurs d’un objet, sa taille, sa forme, sa position, son orientation…, le nombre d’éléments d’une collection peuvent être sujets à variations.
Quand le changement découvert porte sur une (ou plusieurs) propriété(s) d’un objet, il s’agit de définir précisément quelle est la propriété en question et ce qu’elle devient, puis d’appliquer scrupuleusement le nouveau mode d’emploi du fonctionnement de cette fonction dans de nombreuses autres situations.
On peut aussi par la suite inventer des dessins pour le jeu des différences : il faut créer deux images jumelles et modifier volontairement quelques détails (une couleur, une taille, une forme…) dans la deuxième.
transformer
Certains changements entre deux objets portent sur des figures. Pour ces correspondances ponctuelles, en géométrie, on parle de transformations qui comptent entre autres les symétries (axiales, ponctuelles), les translations, les rotations, les homothéties.
La géométrie de transformation approche les figures par l’étude des propriétés invariantes lors de ces transformations.
La coupe, le moustique, la décoration de Noël, … permettent une approche et une utilisation de la symétrie axiale, la tour Eiffel, les poupées russes, … renvoient à l’homothétie, la danse macarena, les pétales de la fleur à la rotation et le chien Chipie à la translation.
des changements particuliers : les fonctions et lois numériques
L’étude des fonctions et des lois numériques occupe une place importante à l’école. Que de temps passé à mémoriser les tables ou à maîtriser les pratiques des techniques opératoires !
Les passages du samedi 17 au lundi 19, du samedi 3 au lundi 5, mais aussi du mardi 13 au jeudi 15, etc. sont les mêmes : 2 perles de plus, donc 2 jours de plus.
Mais aussi 2 € de gain pour la dent perdue grâce à la petite souris (mon porte-monnaie contenant 3 € est passé à 5 €), ou encore 2 bonbons en plus, 2 livres en plus…
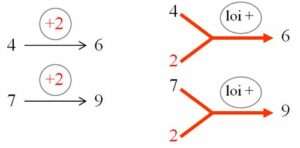
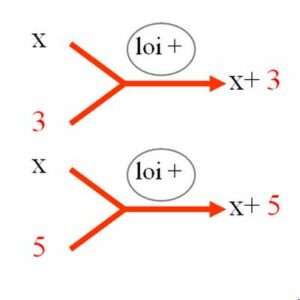
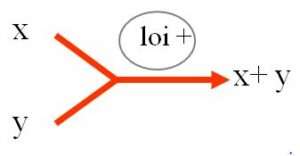
De très nombreux exemples font apparaître, dans des situations très diverses, une remarquable constance dans le changement : 2 de plus que 3, c’est 5. Mais c’est aussi le passage de 13 à 15, de 17 à 19…
La connaissance de cette fonction numérique +2 apporte un véritable pouvoir.
Et il en est de même pour toutes les autres : +3, +5, +10, +25,… +n.
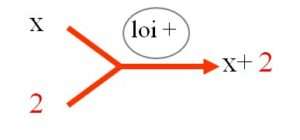
Ainsi la loi de composition appelée addition suppose la maitrise de toutes les fonctions additives +n
 |
 |
 |
 |
l’idée de détermination : si … alors
La date : si c’est écrit en bleu, alors après ce sera en rouge ; si c’est en rouge, alors ce sera blanc ; si c’est blanc, alors ce sera bleu.
Les stylos : si c’est bleu, alors ce sera rose ; si c’est gris, alors ce sera gris.
La date : si c’est en script, alors ce sera en cursive.
S’il pleut, alors l’escargot sort de sa coquille.
Si le feu de circulation est rouge, alors papa arrête la voiture.
Si le feu de circulation est rouge, alors après ce sera vert.
Si le feu est vert, alors papa démarre la voiture.
« Si tu n’es pas sage, alors … », menaces de chantage proférées régulièrement par des adultes à des enfants.
Le « si … alors » également parfaitement maîtrisé par le jeune bébé : si je pleure, alors il ou elle me prendra dans ses bras.
Si c’est mercredi, alors on reste à la maison (pas classe).
Si je descends allongé au toboggan, alors je vais plus loin.
Si j’ai « orange » en comportement, je ne suis pas autonome en dehors de la classe et je n’ai donc pas le droit de sortir seul.*
L’actualisation d’un événement dépend d’une condition. Cette notion de détermination est assez courante dans la vie quotidienne.
Alors, quand elle se présente, pourquoi ne pas la remarquer et s’y arrêter un court instant.
Si le verbe se termine en « er », alors il est du 1er groupe. S’il est du 1er groupe, et s’il est au présent, et (!) s’il est conjugué à la deuxième personne du singulier, alors sa terminaison est « es ».
Toute la conjugaison des verbes en langue française fonctionne sur ce principe du « si … alors ». Il en va de même pour les innombrables règles, et leurs nombreuses exceptions, qui accompagnent l’étude de la langue française.
La notion de fonction est liée à l’idée de détermination. Suivant des règles et un mode d’emploi définis clairement en amont, le changement s’opère systématiquement et immuablement de la même façon : le bleu devient toujours rose, la carré se transforme toujours en triangle, « tourner à droite » est remplacé par « tourner à gauche », 4 –2 de plus –> ce sera toujours 6 (dans le système décimal), etc.
On ne change pas les règles quand la fonction est définie.
Si on veut faire un autre changement, alors il faut changer de fonction.
* pour le fonctionnement des brevets d’autonomie (rouge, orange, vert), voir la partie 1 la recherche/un milieu favorable.
définir la fonction
quel changement ?
Il est essentiel de définir clairement la fonction utilisée ou inventée.
Une fonction est définie comme une relation qui associe chaque élément d’un ensemble de départ appelé objet à un unique élément d’un autre ensemble (ou du même) souvent nommé image.
comment le représenter ?
Pour les jeunes enfants, quand il s’agit de représenter un changement, un sérieux problème se pose : comment distinguer l’élément de départ de celui d’arrivée, l’objet et l’image, le début et la fin, et comment indiquer les différents liens.
A l’oral, il suffit de dire ou de montrer avec la main.
Mais si ceux-ci sont nombreux, les informations s’accumulent mais s’envolent vite et les difficultés apparaissent. Comment conserver toutes ces données ?
Les noter sur une feuille de papier apparaît comme une bonne idée, mais ne réduit pas les difficultés : représenter le temps (avant, après) n’est pas une mince affaire.
Divers procédés sont proposés et testés * :
– emploi de marqueurs : la couleur (bleu pour l’objet, rouge pour l’image), des numéros ( 1 et 2), des étiquettes…
– utilisation de la position spatiale : à gauche (objet), à droite (image), en haut ou en bas,…
La représentation du lien entre éléments fait également l’objet de tâtonnements.
La flèche n’apparaît pas naturellement comme solution intéressante.
* voir partie 2, chapitre 4 « la ducasse »et partie 4, chapitre 2 math non numérique »
définir la fonction avec précision
Comment faire pour définir sans ambiguïté la fonction en question ? Que dire pour faire comprendre ce qu’elle est ?
Il est nécessaire de préciser de quoi on parle :
– le domaine de définition des objets, des antécédents ;
– l’ensemble d’arrivée des images ;
– les liens qui relient ces éléments.
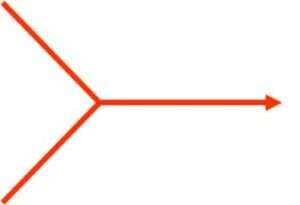
Un schéma général de représentation d’une fonction est mis en place :
une entrée, une sortie et une flèche (relation) qui est nommée ; le nom de l’opérateur en jeu est entouré. C’est le schéma choisi pour représenter un changement.
![]()
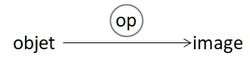

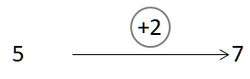
La définition de la fonction peut-être faite en extension en énonçant l’ensemble des couples qui vérifient la relation (le graphe de la fonction), ou en compréhension par une phrase explicative ou par un mode d’emploi, une formule de calcul, une technique opératoire.
La fonction doit être nommée.
On peut en donner une image, la représenter, quelquefois graphiquement.
Pour l’exemple des deux stylos : le changement porte sur la propriété couleur, sur les deux couleurs rose et gris.
Le domaine de définition est {bleu, gris}
L’ensemble d’arrivée est {rose, gris}
Les liens, présentés ici sous forme de diagramme :
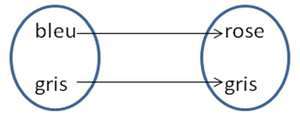
Ou alors comme un ensemble de couples {(bleu,rose), (gris,gris)}
On peut donner un nom à la fonction : f stylo.
Le changement ne peut se faire que dans ce cadre-là. Si j’ai un stylo avec du vert, je ne peux rien faire. A moins de changer les ensembles de définition et d’arrivée de la fonction et d’y ajouter un couple : (vert, …).
Cette fonction ne peut s’appliquer qu’une fois : bleu –>rose –> ?
Là encore, il est possible de changer la fonction et son ensemble de définition.
faire fonctionner les lois
Le livre « Petit-Bleu et Petit-Jaune » raconte une autre histoire de changement : quand les deux amis s’embrassent, ils deviennent verts. C’est à dire :
(bleu, jaune)– s’embrassent–> vert
Le concept opérant « deux choses s’assemblent pour en faire une nouvelle » se retrouve assez régulièrement dans des gestes de la vie quotidienne :
– préparer une tasse de chocolat en mélangeant du lait et du cacao, une boisson rafraichissante avec de la grenadine et de l’eau ;
– faire deux choses l’une après l’autre pour obtenir un résultat : pour pouvoir présenter mon texte libre, j’écris l’histoire puis je fais l’illustration (ou l’inverse) ;
– deux choses sont nécessaires pour en obtenir une troisième : pour avoir le droit de patiner pendant l’activité patinoire, je dois apporter un bonnet et des gants, pour admirer un arc-en-ciel, il faut du soleil et de la pluie ;
– deux choses peuvent être remplacées par une troisième : pour aller à l’école, je peux passer chez ma copine puis aller à l’école, ou alors aller directement à l’école
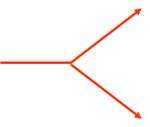
a —> b, puis b —> c ou alors a —> c (idée du raccourci).
composer, décomposer
Associer deux éléments pour en produire un troisième :
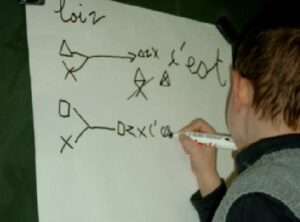 |
Julien crée une nouvelle figure à partir de deux autres : il place la première au-dessus de la deuxième. C’est la loi de composition de figures |
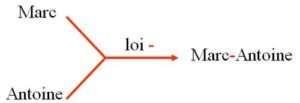 |
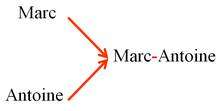
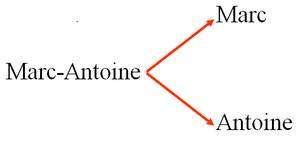
Le prénom Marc-Antoine est composé de deux autres prénoms à l’aide de la loi de composition des prénoms appelée – (trait d’union). |
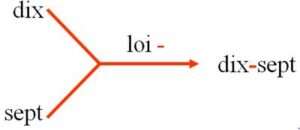 |
pareil pour les noms des nombres |
Il est possible de défaire ce qui a été fait : de décomposer le résultat final pour retrouver les éléments de départ.
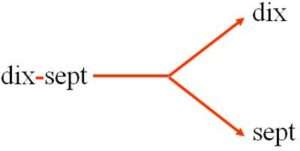 |
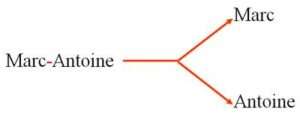 |
Mais est-ce toujours possible dans la réalité ?
Est-il possible d’obtenir à nouveau du lait et de la poudre de cacao à partir du chocolat, comme on le fait pour le dessalement de l’eau de mer avec l’eau douce et le sel ?
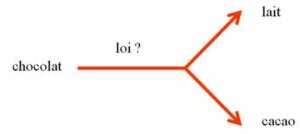
Existe
représenter la loi
La recherche d’une représentation des changements de type composition / décomposition s’oriente vers l’idée de réutiliser des flèches comme pour les fonctions (avant/après)
|
pour la composition : Marc—> Marc-Antoine
|
pour la décomposition : Marc-Antoine—> Marc
|
définir la loi
Comment faire pour définir sans ambigüité la loi de composition en jeu ? Que dire pour faire comprendre ce qu’elle est et comment elle fonctionne ?
Il est nécessaire de préciser de quoi on parle :
| départ | arrivée | lien | |
|
loi de composition loi * |
ensemble de couples d’éléments de E et de F nommé (E x F) |
ensemble d’éléments G |
(a,b) —-> c
|
| loi de décomposition |
ensemble d’éléments | ensemble de couples d’éléments | 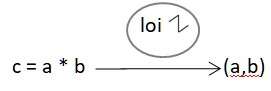 |
– le domaine de définition des éléments concernés ;
– l’ensemble d’arrivée des images ;
– les liens qui relient ces éléments.
La définition de la loi peut-être faite
– en extension en énonçant l’ensemble des triplets (la table de la loi), quand c’est possible :
– ou alors en compréhension par une phrase explicative (exemple : le premier élément au-dessus du deuxième), ou par un mode d’emploi, une formule, une technique opératoire qui permet de calculer l’image.
La loi doit être nommée.
changer le changement
Lorsqu’un changement est constaté, qu’une fonction ou une loi repérée, étudiée et maîtrisée, la curiosité pousse à élargir le champ d’exploration en changeant le changement, en dérogeant à la règle fixée, en modifiant la définition de la fonction ou de la loi pour découvrir des situations nouvelles qui à leur tour deviennent objets de recherches.
les fonctions et les lois
de nouvelles fonctions
En s’inspirant des fonctions découvertes et de leurs propriétés, il est très tentant d’en inventer d’autres.
Par exemple, à partir du changement de place des couleurs du drapeau français, on peut s’interroger sur toutes les possibilités que permet cette situation. Il est possible de chercher d’autres drapeaux tricolores et de leur appliquer la nouvelle fonction découverte, d’imaginer d’autres configurations de drapeaux à deux, quatre… couleurs, avec une disposition spatiale nouvelle : rectangle vertical, cercle, triangle… carré(?), d’élargir les essais à d’autres objets de couleurs.
Le bracelet, après exploration et découvertes diverses, peut donner lieu à l’invention de nouveaux bracelets similaires avec une autre couleur, deux autres couleurs, ou plus, avec un autre agencement, des périodes différentes, ou encore avec une combinaison des deux propriétés…
Un large champ d’investigation est ouvert !
– la date au tableau : utiliser l’écriture en capitales, les chiffres romains, remplacer les mois par leur numéro (le 6/10) ;
– les règles : inventer d’autres règles dont la taille augmente ou diminue régulièrement ;
– les trousses, les stylos : utiliser d’autres couleurs, inventer des situations colorées plus complexes ;
– les couleurs de la date : les changer, imaginer d’autres situations similaires ; chercher d’autres situations de permutation à trois éléments ;
– le drapeau français : changer la disposition spatiale : rectangle vertical, cercle, triangle… carré ?
– le chien, les fleurs, les papillons « Chipie » : inventer d’autres personnages ;
– le dragon : plus de flèches dans le carquois ;
– les cachets : changer leur nombre ;
– le bracelet : un bracelet pareil mais avec d’autres couleurs, avec un autre agencement ;
– les colliers : transformer d’autres colliers longs en colliers courts ;
– le calendrier : étudier d’autres passages ;
– les saisons : la saison avant ;
– la fleur : créer d’autres fleurs (plus ou moins de pétales, des pétales plus ou moins grands, de couleurs différentes,…)
– la montre : d’autres listes de numéros qui changent ; d’autres associations de numéros, d’autres formes de montres ;
– la marche des facteurs : comparer les pas du facteur avec ceux d’autres enfants ;
de nouvelles transformations
– la coupe, le drôle de papa * : changer l’axe de symétrie (vertical, oblique, non rectiligne, curviligne…), modifier les invariants de la symétrie axiale* (la perpendicularité, l’équidistance) ;
– le moustique : des bêtes asymétriques (3 pattes/2 pattes, 4 p/3 p, changements asymétriques sur la longueur, la forme des pattes… ;
– la décoration de Noël dans les rues : en inventer d’autres avec axe horizontal ;
– le chien Chipie : modifier les invariants de la translation** ( direction,sens ou/et longueur du « glissement ») ;
* voir partie 2 « des recherches/drôle de papa » et partie 4 « domaines math/géométrie de transformation« .
** voir partie 4 « domaines math/géométrie de transformation« .
de nouvelles lois
– Petit Bleu et Petit Jaune : composer, décomposer d’autres couleurs ;
– le chocolat : tester d’autres mélanges avec différents ingrédients ou associations (lait, eau, sel, sucre, sirop…), réfléchir à la décomposition ;
– l’arc-en-ciel, à la patinoire : trouver d’autres situations dans lesquelles un événement est dépendant de deux conditions (la pousse des champignons/ l’eau + soleil), ou bien deux causes qui entraînent une conséquence ;
– « Marie-Paule » : répertorier d’autres prénoms composés, d’autres mots composés (porte-manteaux, …)
– 27, c’est 20 et 7 : d’autres compositions additives (30 + 6, c’est 36), multiplicatives (4 x 3, c’est 12,) et décompositions numériques (145, c’est 100 + 40 +5, ou 140 + 5, ou 100 + 45) , (10, c’est 7 + 3, mais aussi 8 +2) ;
réitérer le changement
Il est également possible de composer certaines fonctions ou transformations en les répétant une ou plusieurs fois :
![]()
![]()
Ou en les composant entre-elles :
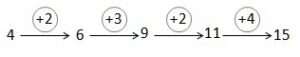
![]()
![]()
L’étude de ces chaînes de fonctions ou de transformations met en évidence l’importance de la réduction et de l’équivalence des chaînes.
Soit * la loi de composition qui permet de mettre bout à bout, ici plusieurs fonctions
![]()
L’ordre d’effectuation des actions est-il important ?
Peut-on réduire cette chaîne ?
Quelle en sera la fonction composée équivalente ?
annuler le changement : le retour au point de départ
Les variations de couleurs d’un objet, de taille, de forme, de position, d’orientation…, du nombre d’éléments d’une collection peuvent-elles être annulées ? Le retour en arrière est-il possible ?
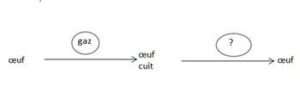
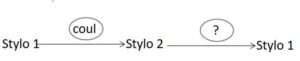
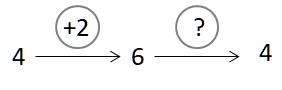
Existe-t-il un changement qui permet de retrouver la figure initiale transformée par une symétrie, une rotation, … ?


de l’acte à la pensée
penser le changement, inventer de nouveaux changements abstraction
créations formelles : et si …
explorations
invariances
texte
c’est pareil ! des concepts
conceptualisations