préambule

C’est la technique de la recherche libre mathématique à partir d’événements tirés de la vie courante, de la classe, de créations ou de situations abstraites qui est choisie pour permettre la construction des savoirs. Elle est issue de la pédagogie Freinet et corroborée par les apports du (socio)constructivisme** (Bruner, Vygotski) et de la Théorie de l’Autodétermination** (Deci & Ryan).
Elle place  l’enfant dans des situations problématiques qui l’obligent à une réelle activité mathématique, activité qui va au-delà des simples constatations et découvertes de notions mathématiques. En effet, la seule fréquentation de situations recelant des notions maths ne suffit pas.
C’est lors du processus de résolution que des choix de stratégies sont faits, que la montée naturelle en abstraction et la symbolisation accompagnent la recherche des représentations appropriées, témoins de l’avancée, de l’état de la réflexion en cours et conformes au but poursuivi.
C’est dans cette montée en abstraction et dans son aboutissement que se construit la culture mathématique.
C’est la communication au groupe classe (présentation de la recherche), et les échanges à l’intérieur de celui-ci, qui favorisent la conceptualisation et la transférabilité des savoirs.
Là est la véritable activité mathématique, dans un processus de résolution qui aboutit à des savoirs intégrés parce que construits et porteurs de sens.

*voir partie 1, chapitre 7 : la recherche libre mathématique

**voir partie 1, chapitre 3 : apprendre

processus de résolution et montée en abstraction

choix de la démarche de résolution : les représentations

  Une situation singulière problématique apparaît. Après discussion, un premier défi à relever  est lancé, initiant ainsi une ébauche de projet de recherche. Il s’agit alors de construire une démarche de résolution : essayer de représenter l’événement initial, d’une façon ou d’une autre, puis progressivement, tout au long de la recherche, de faire des choix : quels sont les éléments pertinents qu’il faut prendre en compte pour avancer dans la réflexion, quels sont ceux, inutiles, qu’il faut écarter. Le processus de résolution passe alors par le choix de représentations adéquates qui rendent visible l’évolution de la pensée du chercheur.
Le choix d’une représentation traduit et actualise l’état de réflexion, de compréhension du moment. Et réciproquement, la manipulation, l’observation des représentations produites nourrissent à leur tour l’évolution de la recherche.

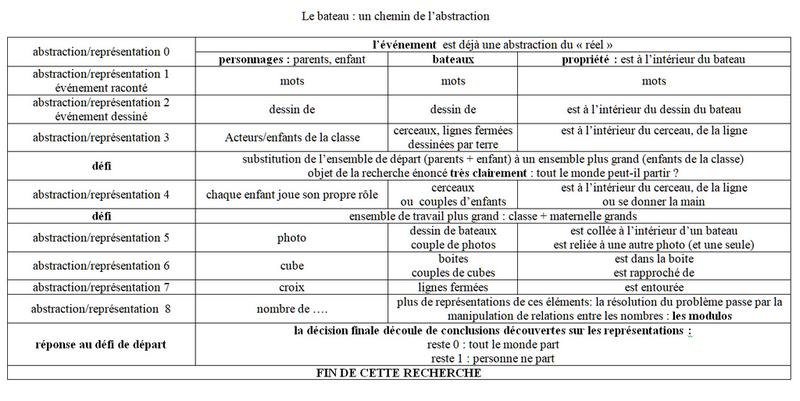
Dans la recherche « le bateau » (voir partie 2), la nouvelle que nous a transmise l’enfant de six ans est déjà une abstraction sérieuse de ce qu’il a réellement vécu, vu, ressenti le dimanche précédent au bord de l’eau. De nombreuses caractéristiques ont été laissées de côté parce que non pertinentes par rapport aux contraintes de l’exercice « dire sa nouvelle » *: être le plus concis et clair possible, dire où, quand, comment, qui ? …, respecter le temps de parole limité…

Les éléments principaux sont racontés : les parents, l’enfant, le bateau utilisé, les bateaux, le lac, le beau temps, mais aussi les émotions ressenties (plaisir, appréhension).
La question de l’enseignant problématise la situation et provoque l’incertitude. Il faut agir et choisir les premiers éléments qui seront pertinents pour la résolution du problème : les enfants de la classe, leur répartition par bateau.
L’obligation d’être à deux  pour pouvoir partir amène un nouvel élément : la paire et une contrainte supplémentaire qui va au-delà de la première intuition « S’il y a assez de bateaux, tout le monde partira ». Il suffirait (?) alors de connaitre le nombre de bateaux. Le défi lancé (« Tous les enfants de la classe auraient-ils pu partir en même temps ? ») complique la situation. Il oblige à représenter une propriété : « être à deux à l’intérieur d’un bateau » et à prendre en compte un élément supplémentaire : est-ce que ça va tomber « juste », ne va-t-il pas en rester un tout seul sur le bord ?
Pour relever ce défi, il est nécessaire d’adopter une démarche de résolution : c’est la re-présentation (présentation à nouveau) de la situation (et de ses évolutions) qui est choisie : par le dessin, par le jeu théâtral (jouer physiquement les choses), par le collage, l’utilisation d’objets (craies, cerceaux, jetons), puis de signes, de symboles (croix, nombres, …)

*voir partie 1, chapitre 6 : un milieu favorable à la recherche

représentations et abstraction

  Dans la recherche « le bateau« , les éléments principaux (par apport à l’objet de la recherche) sont identifiés : les enfants, les bateaux, et des notions moins « concrètes » : les propriétés « est à l’intérieur du bateau » et « être par deux ».

A l’origine de la recherche « la marche des facteurs » , Sandrine raconte un événement vécu qui lui tient à cœur : son père est facteur et il a participé à l’épreuve. C’est une première représentation orale du réel. Elle a apporté une photo et un article de journal « la Voix du Nord » (deuxième représentation). Puis après de nombreuses réponses aux questions posées, c’est sur les pas du facteur que l’on s’est focalisé. Troisième représentation de la réalité très expurgée : elle joue les grands pas de son père.
On pense à ce moment à Bertrand (le plus jeune de la classe unique) et à ses tout petits pas, et peu à peu une recherche nait.
Nouvelle représentation : Sandrine (puis moi), on joue les pas du facteur  et Bertrand fait ses propres pas.
Représentation suivante : les pas sont tracés à la craie.
L’objet de la recherche est posé : si le facteur fait 2,3 … x pas, combien en fera Bertrand ?
Les représentations vont se succéder au fur et à mesure de l’avancée dans la recherche : les pas sont représentés par des segments de droites en taille réelle, puis par souci pratique en taille réduite avec respect des proportions (sur papier quadrillé), puis sur papier libre. Le souci de dessiner des pas de longueur égale disparaît peu à peu – cette contrainte n’apparaît pas pertinente pour la recherche – au profit du seul respect du nombre de pas de Bertrand.
Par souci d’économie et de rapidité, les pas deviennent des croix, des croix et des nombres puis des nombres.
Des tableaux de nombres, puis des listes ordonnées sont utilisées pour répondre au défi : x pas de facteurs —> y pas de Bertrand.
C’est l’exploration des tableaux de résultats* qui finalement aboutit à une liste de couples de nombres et à la maîtrise de la fonction x4 (construction et utilisation de la table, et d’une technique opératoire pour les nombres plus grands). C’est la réponse apportée au défi initial.

  Dans la recherche « la ducasse », la collecte et la conservation des données s’accompagne d’un sérieux écrémage de la réalité vécue fortement sur le plan émotionnel. Pour relever le double défi qui s’impose (clarifier la situation pour chaque enfant de la classe et produire un document sur la ducasse pour les correspondants), il s’agit  de représenter des propriétés, des relations. Les outils de résolution construits (diagrammes, tableau cartésien) s’avèrent extrêmement efficaces.

    Chaque avancée dans le cheminement de la recherche se traduit par l’adoption d’une nouvelle représentation qui révèle à son tour un changement de niveau d’abstraction : on laisse de côté certaines caractéristiques de l’événement devenues inutiles au profit d’autres plus pertinentes pour la résolution du problème. Peu à peu le chercheur s’approche de l’essence même du problème qui dans le cas des pas du facteur est le recours aux nombres et à une relation particulière entre eux : la fonction numérique y = 4x. Pour « la ducasse », la procédure experte de résolution consiste à utiliser un diagramme ou un tableau cartésien.

Réciproquement, l’adoption d’une nouvelle représentation témoigne de l’accès à un nouveau niveau d’abstraction.
Représentation et abstraction apparaissent comme des notions indissociablement liées.
La conscience d’abstraire est importante : elle participe au renforcement du sens de l’activité et de son histoire : on sait ce que l’on fait et pourquoi on le fait.

* tout cela est développé dans l’onglet  » « domaines math «  » en particulier dans les sous-domaines « fonctions »

concepts

concept de deuxième niveau

Le processus de résolution de situations  spécifiques problématiques se termine avec la production d’un savoir-faire opératoire. Le concept apparait sous son double aspect : une procédure d’élaboration et un produit final.
Pour « le bateau« , il s’agit de déterminer les éléments constitutifs du problème et de les représenter, puis de les grouper par deux et enfin, selon le reste de l’opération effectuée (o ou 1) de répondre au questionnement initial.
D’autres situations singulières similaires sont ou seront étudiées dans la classe.

D’autres situations singulières :

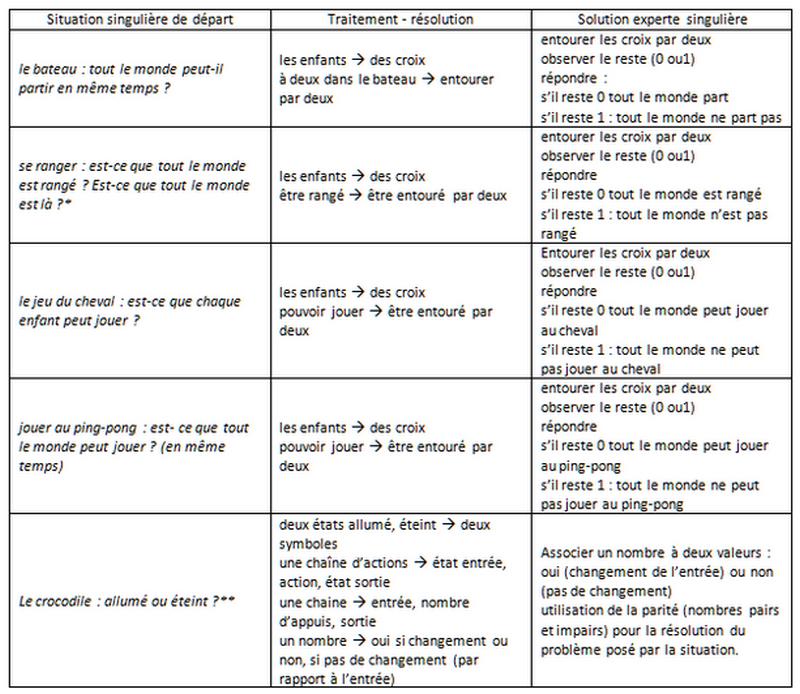
*Le jour de la rentrée, tout le monde se range avant d’entrer en classe. Nous sommes vingt enfants de 7/9 ans. On a remarqué que quand tout le monde est là, tout le monde est rangé par deux, personne ne reste tout seul. Les enfants en ont conclu que quand tout le monde est rangé, tout le monde est là. (d ’où l’intérêt du groupement par deux et de son reste).
L’hypothèse s’est avérée fausse par la suite…et a permis d’autres investigations.

** voir partie 4, les modulos.
Ce crocodile, un petit jouet, a été rapporté et présenté par un enfant lors de la présentation d’objets. En appuyant dessus, il s’allumait et s’éteignait. L’intérêt était de deviner quel était l’état final du crocodile après 18, 37, X appuis,… Je les avais épatés en répondant correctement et systématiquement à toutes les situations. Le défi était de comprendre, comme je n’étais pas magicien, comment je faisais…

élargissement des concepts de deuxième niveau

D’autres situations singulières* comme jouer au dromadaire, danser la macarena, les mois de l’année aboutissent à l’élaboration d’autres concepts de même niveau : le modulo 3, le modulo 4, le modulo 12…

Une autre réflexion sur ces nouveaux concepts entraine, avec de nouvelles montées en abstraction, l’apparition du concept d’un ordre supérieur : le modulo.

Ce long processus de recherche libre se déroule dans tous les domaines de la mathématique, de la notion de propriété aux lois de composition, aux structures algébriques (groupe…), en passant par les relations, les fonctions et les transformations géométriques.

le non numérique,un lieu de symbolisation et d’abstraction

un monde fécond à ne pas négliger

Le non numérique, lieu de symbolisation : entendre ce qui est dit